Ingin tahu lebih dalam tentang apa itu kurva dalam matematika? Temukan penjelasan lengkap tentang konsep kurva, berbagai jenis kurva, dan penerapannya dalam berbagai bidang.
Kurva dalam matematika bukan sekadar garis yang melengkung, melainkan entitas kompleks yang memiliki berbagai aplikasi dan interpretasi. Pada dasarnya, “apa itu kurva dalam matematika” merujuk pada garis yang tidak terputus dan tidak linear, yang menggambarkan hubungan antara dua variabel dalam suatu sistem koordinat. Kurva ini bisa muncul dalam bentuk fungsi matematika, grafik data, atau bahkan dalam model geometris yang lebih abstrak. Dalam konteks ini, kurva memainkan peran krusial dalam analisis data dan teori matematika, memungkinkan kita untuk memvisualisasikan dan memahami pola yang tidak bisa dijelaskan hanya dengan garis lurus. Selain itu, kurva juga memiliki aplikasi luas di bidang teknik, fisika, dan ekonomi, di mana mereka membantu dalam model prediksi dan analisis kompleks.
Jenis-jenis Kurva dalam Matematika
Ada beberapa jenis kurva yang umum ditemukan dalam matematika:
- Kurva Linier
Kurva linier merupakan bentuk paling sederhana, di mana hubungan antara dua variabel direpresentasikan oleh garis lurus. Persamaan umum kurva linier adalah 𝑦 = 𝑚𝑥 + 𝑐, di mana 𝑚 adalah kemiringan dan adalah konstanta.
- Kurva Kuadrat
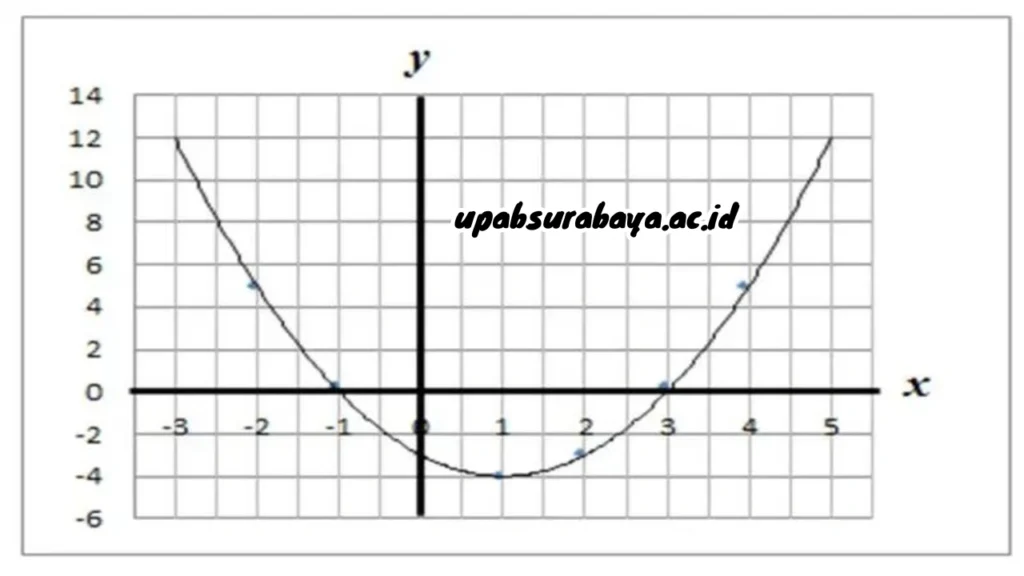
Setelah kurva linier kini perhatikan gambar kurva parabola berikut merupakan grafik dari fungsi kuadrat yang berbentuk parabola yang direpresentasikan oleh persamaan 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐. Kurva ini sering digunakan untuk menggambarkan gerak dalam fisika, seperti gerak peluru atau benda yang dilempar.
- Kurva Eksponensial
Kurva eksponensial memperlihatkan pertumbuhan yang sangat cepat atau peluruhan yang signifikan. Persamaan umum kurva ini adalah y=a ⋅ e bx, di mana 𝑎 dan 𝑏 adalah konstanta, serta 𝑒 adalah bilangan Euler. Kurva eksponensial banyak digunakan dalam bidang biologi dan keuangan untuk memodelkan populasi atau investasi.
- Kurva Logaritmik
Kurva logaritmik adalah kebalikan dari kurva eksponensial. Bentuknya cenderung naik tajam di awal namun melambat seiring bertambahnya nilai variabel. Persamaan umumnya adalah 𝑦 =𝑎⋅log (𝑥).
- Kurva Parametrik
Kurva parametrik tidak direpresentasikan oleh satu fungsi, melainkan oleh dua fungsi yang menggambarkan variabel x dan 𝑦 secara terpisah sebagai fungsi dari parameter ketiga, sering kali waktu (𝑡).
Aplikasi Kurva dalam Kehidupan Nyata
Kurva memiliki banyak aplikasi di berbagai bidang. Dalam fisika, kurva digunakan untuk menggambarkan lintasan gerak benda, seperti orbit planet atau lintasan peluru. Dalam ekonomi, kurva digunakan untuk memodelkan hubungan antara permintaan dan penawaran, atau untuk memprediksi pertumbuhan ekonomi. Di bidang teknik, kurva digunakan dalam desain mesin, analisis struktur, dan banyak lagi.
Misalnya, dalam bidang ekonomi, kurva permintaan (Demand Curve) menggambarkan hubungan antara harga suatu barang dengan jumlah yang diminta konsumen. Kurva ini biasanya melengkung ke bawah, menunjukkan bahwa saat harga naik, permintaan akan menurun.
Kurva dan Analisis Data
Dalam analisis data, kurva digunakan untuk menggambarkan tren atau pola dalam kumpulan data besar. Misalnya, kurva distribusi normal digunakan untuk memodelkan distribusi probabilitas dalam statistik. Kurva ini penting dalam analisis regresi, di mana hubungan antara variabel dependen dan independen dapat divisualisasikan melalui kurva terbaik yang sesuai dengan data.
Memahami apa itu kurva dalam matematika membuka wawasan luas terhadap berbagai konsep dan aplikasinya di dunia nyata. Baik dalam sains, teknik, maupun ekonomi, kurva memainkan peran penting dalam pemodelan dan analisis berbagai fenomena. Kurva tidak hanya membantu kita memvisualisasikan hubungan antar variabel, tetapi juga memungkinkan kita untuk membuat prediksi yang lebih akurat dan menyusun strategi berdasarkan data yang ada.